Regression linéaire au sens des moindres carrés¶
Imaginons que nous souhaitions à partir des données ($x_i$ et $y_i$), trouver la fonction qui a permis de générer ces données.
Il faut d'abord une fonction pour générer les valeurs $y_i$ à partir de $x_i$.
Voir le code ci-dessous pour la création de la fonction $y=2x+3$.
def mafonction(x):
y=2*x+3
return y
mafonction(1)
Ensuite, il nous suffit de créer les $x_i$. Nous allosn en créer $M=10$.
import numpy as np
M=10 #nombres d'échantillons ou d'individus ou variables explicatives
X=np.zeros((M,1)) # les échantillons ou individus ou variables explicatives
for i in range(0,M):
X[i,0]=i
print(X)
Finalement, nous créons les $y_i$ associés aux $x_i$.
Y=np.zeros((M,1)) # les prédictions ou variables expliquées
for i in range(0,M):
Y[i,0]=mafonction(i)
print(Y)
Nous pouvons affichier $Y=f(X)$
import matplotlib.pyplot as plt
plt.plot(X,Y)
plt.show()
On veut, à partir des echantillons X et Y, trouver le coefficient directeur (a) et l'ordonnée à l'origine (b) de la droite liant ces 2 variables.
On veut trouver $\widehat{Y_{i,0}}=a \times X_{i,0} + b$.
A la place de $a$ et $b$, nous utiliserons $W_0$ et $W_1$:
$$\widehat{Y_{i,0}}=W_0 \times X_{i,0} + W_1$$
Pour des raisons d'écriture et faciliter les calculs par la suite, nous allons considérer que l'ordonnée à l'origine dépend des données (X) mais nous imposerons que X{i,1} soit toujours 1 (voir ci-dessous) : $$\widehat{Y{i,0}}=W0 \times X{i,0} + 1 \times W_1=W0 \times X{i,0} + X_{i,1} \times W_1$$
X=np.zeros((M,2)) # les échantillons ont maintenant 2 colonnes
for i in range(0,M):
X[i,0]=i
X[i,1]=1 #toujours 1
print(X)
La prédiction $\widehat{Y_{i,0}}$ peut maintenant s'écrire comme le produit scalaire du vecteur $X_i$ et $W$
$$\widehat{Y_{i,0}}=W_0 \times X_{i,0} + X_{i,1} \times W_1=X_i.W$$
Le problème¶
Le problème est donc de trouver $W_0$ et $W_1$ tel que la prédiction ($\widehat{Y_{i,0}}$) soit proche de la valeur désirée ($Y_{i,0}$). Autrement dit, il faut minimiser l'écart (ou l'erreur) entre $\widehat{Y_{i,0}}$ et $Y_{i,0}$.
Le problème : $$ \min_W \dfrac{1}{2}L(X,Y;W)$$
Avec L : $$L(X,Y;W)=\sum_i^M (Y_i- \widehat{Y}_i)^2$$ La fonction $L$ consiste à calculer la somme des erreurs au carrè.
Cela peut se ré-écrire à l'aide de la norme L2 élevée au carré. $$L(X,Y;W)=||Y-\widehat{Y}||^2_2$$
$$L(X,Y;W)=||Y-XW||^2_2=(Y-XW)^2=(Y-XW)^T(Y-XW)$$ On développe L : $$L(X,Y;W)=Y^TY-W^TX^TY-Y^TXW+W^TX^TXW$$ $$L(X,Y;W)=Y^TY-2W^TX^TY+W^TX^TXW$$
Pourquoi $\dfrac{1}{2}$ devant L dans le problème ?
Cela va simplifier les calculs par la suite. Par forcément ici mais par la suite avec les neurones.
Résolution optimale (Analytique)¶
On veut trouver W qui minimise la fonction L alors on dérive et l'on trouve où la dérivée s'annule. $$\dfrac{\partial L}{\partial W} = 0 $$ Dérivée partielle de L
La dérivée partielle de L est simple il s'agit de dériver un polynome de degré 2. $$\dfrac{\partial L}{\partial W} = -2X^TY+2X^TXW $$ Comme on a multiplié par $\dfrac{1}{2}$ alors on peut écrire : $$\dfrac{\partial L}{\partial W} = -X^TY+X^TXW $$ $$\dfrac{\partial L}{\partial W} = X^T(XW-Y) $$
Trouver W $$\dfrac{\partial L}{\partial W} = 0 $$ $$\dfrac{\partial L}{\partial W} = -X^TY+X^TXW =0$$
Résultat :$$W=(X^TX)^{-1}X^TY$$
Maintenant on peut calculer W en python :
Implémentation¶
#On calcule W
XT= X.transpose() #Transposé de X
prodX =XT.dot(X) #Produit matriciel
invprodX=np.linalg.inv(prodX) #inversion de matrice
prodxx=invprodX.dot(XT)
W =prodxx.dot(Y)
print(W)
On peut maintenant calculer la prédiction ($\widehat{Y}$): $$\widehat{Y_{i,0}}=X_{i,0}.W$$ Le vecteur de prédictions pour tous les echantillons s'écrit: $$\widehat{Y}=X.W$$
Ypred=X.dot(W)
print(Ypred)
On peut calculer l'erreur entre la valeur réelle et la prédiction: $$L(X,Y;W)=\dfrac{1}{2}\sum_i^M (Y_i- \widehat{Y}_i)^2$$ $$L(X,Y;W)=\dfrac{1}{2}||Y-\widehat{Y}||^2_2$$
vecerreur=Y-Ypred #vecteur d'erreurs
normeL2=np.linalg.norm(vecerreur,2) #norme du vecteur
erreur=0.5*(normeL2**2) # exponentiation au carré
print(erreur)
On peut maintenant afficher $Y$ et $\widehat{Y}$:
plt.plot(X[:,0],Y,'red')
plt.plot(X[:,0],Ypred,'blue')
plt.show()
Conclusion¶
Voilà, nous avons construit une fonction mathématique qui modélise les données d'entrées (X et Y).
Nous avons trouvé $$W_0=2 \text{ et } W_1=3$$ Nous avons retrouvé la fonction 2x+3 qui nous avait servi à générer nos données.
Ce qu'il fallait démontrer
A faire par les étudiants¶
Remplacer la fonction "mafonction" par la fonction mathématique $2x+3+Random$ et recalculer $W$ et l'erreur. Remplacer la fonction "mafonction" par la fonction mathématique $2x^2+3$ et recalculer $W$ et l'erreur. Conclure sur la limite du modèle linéaire.
#à faire par les étudiants
Résolution itérative¶
La résolution analytique peut être délicate parfois car elle impose d'inverser la matrice X qui peut être de grande taille.
Une résolution approchée peut être interessante.
Nous allons voir la résolution par descente de gradient.
Un gradient n'est rien d'autre qu'une dérivée à plusieurs dimensions, nous avions calculué le gradient de notre fonction d'erreur ($L$) par rapport à $W$ :
$$\dfrac{\partial L}{\partial W} = X^T(XW-Y) $$ L'algorithme de la descente de gradient cherche à diminiuer le gradient progressivement jusqu'à trouver où le gradient s'annule. Pour diminiuer le gradient il suffit de modifier $W$ dans le sens opposé du gradient. $$W^{t+1}=W^{t}-\alpha. \dfrac{\partial L}{\partial W}$$
$W^{t+1}$ est la nouvelle valeur de $W$
$\alpha$ appelé pas de gradient ou pas d'apprentissage, est un réel représentant la vitesse à la quelle l'algorithme descend la pente du gradient (par exemple : $\alpha$=0.001)
nbiter=20
alpha=0.001
W=np.zeros((2,1))
for t in range(0,nbiter):
ecart=X.dot(W)-Y
normeL2=np.linalg.norm(ecart,2) #norme du vecteur
erreur=0.5*(normeL2**2) # exponentiation au carré
print(erreur)
XT=X.transpose()
gradW=XT.dot(ecart) #calcul du grdient
W=W-(alpha*gradW)# mise à jour des poids
print(W)
Ypred=X.dot(W)
vecerreur=Y-Ypred #vecteur d'erreurs
normeL2=np.linalg.norm(vecerreur,2) #norme du vecteur
erreur=0.5*(normeL2**2) # exponentiation au carré
print(erreur)
plt.plot(X[:,0],Y,'red')
plt.plot(X[:,0],Ypred,'blue')
plt.show()
A faire par les étudiants¶
Jouer avec $\alpha$ et $nbiter$ et regarder l'impact sur l'erreur
Neurone Artificiel¶
Un neurone artificiel peut être représenté par le diagramme suivant :

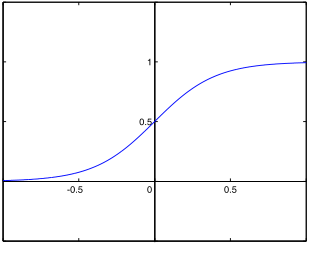
$h$ est une fonction non linéaire aussi appeler fonction d'activation. La fonction sigmoide (sig) ou la fonction tangeante hyperbolique (tanh) sont souvent utilisées comme fonction d'activation. Nous verrons par la suite l'allure de ces 2 fonctions. Pour l'instant, voyons ce qui change dans notre problème par rapport à la regression linéaire : On veut calculer l'erreur entre la valeur réelle et la prédiction: $$L(X,Y;W)=\dfrac{1}{2}\sum_i^M (Y_i- \widehat{Y}_i)^2$$ $$L(X,Y;W)=\dfrac{1}{2}||Y-\widehat{Y}||^2_2$$
On peut maintenant calculer la prédiction ($\widehat{Y}$): $$\widehat{Y_{i,0}}=h(X_{i,0}.W)$$ Le vecteur de prédictions pour tous les echantillons s'écrit: $$\widehat{Y}=h(X.W)$$
Le problème : $$ \min_W \dfrac{1}{2}L(X,Y;W)$$
$$L(X,Y;W)=\dfrac{1}{2}||Y-h(X.W)||^2_2$$
La seule différence est donc la fonction $h$ mais cela a une grande importance ....
On veut trouver W qui minimise la fonction L alors on dérive et l'on trouve où la dérivée s'annule. $$\dfrac{\partial L}{\partial W} = 0 $$
Résoudre l'équation ci-dessus de manière analytique est difficile, vous pouvez essayer pour vous en convaincre. Un résolution approchée par descente de gradient reste néanmoins possible. Il suffit pour cela de calculer : $$\dfrac{\partial L}{\partial W}$$
Calcul de la dérivée partielle de L¶
On cherche la dérivée suivante : $\dfrac{\partial L}{\partial W_0} $ L est une composition de fonctions alors sa dérivée s'appuie sur la chaine de dérivation suivante : Soit $q(p(W_0))$ alors $$\dfrac{\partial q}{\partial W_0} = \dfrac{\partial q}{\partial p} \dfrac{\partial p}{\partial W_0}$$ Calcul de la dérivée partielle
$q_1=L_i=\dfrac{1}{2}(Y_i-\widehat{Y_i})^2$ et $p_1=Y_i-\widehat{Y_i}$ donc $q_1=\dfrac{1}{2}(p_1)^2$
$\dfrac{\partial q_1}{\partial W_0} = \dfrac{\partial q_1}{\partial p_1} \dfrac{\partial p_1}{\partial W_0}$=$\dfrac{1}{2}*2*p_1 \dfrac{\partial p_1}{\partial W_0}=(Y_i-\widehat{Y_i})\dfrac{\partial p_1}{\partial W_0}$
- $p_1=q_2=(Y_i-\widehat{Y_i})$ et $p_2=\widehat{Y_i}$ donc $q_2=(Y_i-p_2)$
- $\dfrac{\partial q_2}{\partial W_0} = \dfrac{\partial q_2}{\partial p_2} \dfrac{\partial p_2}{\partial W_0}$=$-1*\dfrac{\partial p_2}{\partial W_0}$
- $p_2=q_3=sig(z_i)$ et $p_3=z_i$ donc $q_3=sig(p_3)$
$\dfrac{\partial q_3}{\partial W_0} = \dfrac{\partial q_3}{\partial p_3} \dfrac{\partial p_3}{\partial W_0}$=$sig'(z_i)*\dfrac{\partial p_3}{\partial W_0}$
$p_3=q_4=z_i$ et $p_4=z_i=X_{i,0}*W_0+X_{i,1}*W_1$ donc $q_4=p4$
- $\dfrac{\partial q_4}{\partial W_0} = \dfrac{\partial p_4}{\partial W_0}$=$X_{i,0}$
Résultat Final : $$\dfrac{\partial L_i}{\partial W_0}= -(Y_i-\widehat{Y_i})sig'(z_i)X_{i,0}$$ $$\dfrac{\partial L_i}{\partial W_n}= -(Y_i-\widehat{Y_i})sig'(z_i)X_{i,n}$$
Où $sig'(z)$ est la dérivée de sig(z).
La version matricielle peut s'écrire : $$\dfrac{\partial L}{\partial W} =- X^T(Y-\widehat{Y}) * sig'(Z) $$ Avec $*$ le produit d'hadamard élément par élément.
Version matricielle de la descente de gradient avec une fonction sigmoid¶
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def derivative_sigmoid(x):
return sigmoid(x) * (1-sigmoid(x))
def gradient (X,Y,W,pas,nbiter,M,maxy) :
for t in range (0,nbiter):
Z=X.dot(W)
Ypred=sigmoid(Z)
ecart=Y-Ypred
derivesig=derivative_sigmoid(Z)
XT=X.transpose()
#Haddamart product
ecartderive=np.multiply(ecart,derivesig)
grad=-XT.dot(ecartderive)
W = W -pas*grad
normeL2=np.linalg.norm(ecart,2) #norme du vecteur
err=0.5*(normeL2**2) # exponentiation au carré
print('Itération numéro ',t)
print('Erreur : ',err)
return W, err
Classification avec la fonction sigmoid¶
Génération d'un ensemble de données :
def get_datasetv1():
"""
Method used to generate the dataset
"""
# Numbers of row per class
row_per_class = 100
# Generate rows
sick = np.random.randn(row_per_class, 1) - 2
healthy = np.random.randn(row_per_class, 1) +2
ones = np.ones((2*row_per_class,1))
features = np.vstack([sick, healthy])
features=np.hstack([features,ones])
targets=np.zeros((2*row_per_class,1))
targets[0:row_per_class,0]=0
targets[row_per_class:2*row_per_class,0]=1
return features, targets
X,Y=get_datasetv1()
M=X.shape[0]
print('M :',M)
maxx=X.max()
maxy=Y.max()
X[:,0]=X[:,0]/maxx
Y/=maxy
plt.plot(X[:,0],Y,'ro')
plt.show()
Appel à la fonction gradient¶
W=np.zeros((2,1))
pas=0.1
nbiter=20
print('Pas :',pas)
print('Nombre itération : ',nbiter)
W, error =gradient(X,Y,W,pas,nbiter,M,maxy)
prediction=sigmoid(X.dot(W))
bonneclassif=np.mean(Y==np.round(prediction))
print("Taux de bonnes classifications=",bonneclassif)
plt.plot(X[:,0]*maxx,Y*maxy,'ro',color='red')
plt.plot (X[:,0]*maxx,prediction*maxy,'ro',color='blue')
plt.show()
Application à la classification de piétons¶
Lecture des images¶
# Vous devez installer la librairie imageio
# pip install imageio
import imageio
from skimage.transform import resize
import warnings
warnings.filterwarnings("ignore")
def readData(dirimg):
nbfiles = 200
halfnbfiles=int(nbfiles/2)
resizew=28
resizeh=14
featuresize=resizew*resizeh
print("nb files=",nbfiles)
features = np.zeros((nbfiles, featuresize))
veclabels = np.zeros((nbfiles, 1))
images = np.zeros((nbfiles, 128,64))
for i in range(1,halfnbfiles+1):
image = imageio.imread(dirimg + '/' + "pos"+str(i)+".jpg")
images[i-1]=image
image = resize(image, (resizew, resizeh))
features[i-1, :] = image.reshape((featuresize))
veclabels[i-1] = 1
for i in range(1,halfnbfiles+1):
image = imageio.imread(dirimg + '/' + "neg"+str(i)+".jpg")
images[i+halfnbfiles-1]=image
image = resize(image, (resizew, resizeh))
features[i+halfnbfiles-1, :] = image.reshape((featuresize))
veclabels[i+halfnbfiles-1] = 0
#on rajoute le biais
ones = np.ones((nbfiles,1))
features=np.hstack([features,ones])
nbtrain=int(nbfiles * 0.75)
nbtest=int(nbfiles * 0.25)
setindex=[]
for i in range(0,nbfiles):
setindex.append(i)
np.random.shuffle(setindex)
trainfeatures=features[setindex[0:nbtrain]]
testfeatures=features[setindex[nbtrain:nbtrain+nbtest]]
trainlabels=veclabels[setindex[0:nbtrain]]
testlabels=veclabels[setindex[nbtrain:nbtrain+nbtest]]
trainimages=images[setindex[0:nbtrain]]
testimages=images[setindex[nbtrain:nbtrain+nbtest]]
return (trainfeatures, trainlabels,testfeatures,testlabels,trainimages,testimages)
#Un example pour la classif avec les pietons
dirimg="./pieton"
trainfeatures, trainlabels,testfeatures,testlabels,trainimages,testimages=readData(dirimg)
X=trainfeatures
Y=trainlabels
images=trainimages
#Affiche l'image en basse résolution que l'on utilise pour la classification
plt.imshow(X[0,0:28*14].reshape((28, 14)),
interpolation='nearest',
cmap='gray')
plt.show()
#Affiche l'image originale
plt.imshow(images[0].reshape((128, 64)),
interpolation='nearest',
cmap='gray')
plt.show()
#Affiche l'image en basse résolution que l'on utilise pour la classification
plt.imshow(X[100,0:28*14].reshape((28, 14)),
interpolation='nearest',
cmap='gray')
plt.show()
#Affiche l'image originale
plt.imshow(images[100].reshape((128, 64)),
interpolation='nearest',
cmap='gray')
plt.show()
print(X[0,1:10])
nbdim=len(X[i,])
print("dimension de x=",nbdim)
print(Y[0,:])
print(Y.shape)
print(X.shape)
print(testlabels.shape)
print(testfeatures.shape)
Application directe de la version matricielle de la descente de gradient¶
A vous de jouer, classifier les images de piétons¶
Faire un programme dans Spyder qui classifie les images de piétons. Vous apprendrez sur les données suivantes : X=trainfeatures Y=trainlabels Afficher l'erreur et le taux de bonnes classifications par itération.
Tester votre prédicteur sur : X=trainfeatures Y=trainlabels Afficher l'erreur et le taux de bonnes classifications
Puis sur Tester votre prédicteur sur : X=testfeatures Y=testlabels Afficher l'erreur et le taux de bonnes classifications par itération.
Le but est d'évaluer la capacité du prédicteur à prédire sur de nouvelles données (jamais vue)
Ensuite une fois que vous avez atteint un bon taux de classification passer à la suite.
L'erreur quadratique vs cross entropy¶
Minimiser l'erreur quadratique avec une fonction d'activation de type sigmoide rend le problème d'optimisation non-convexe. Une manière classique de contourner ce problème est de minimiser la cross entropy. $$L_i=-(Y_i \log (\widehat{Y_i}) + (1-Y_i) \log( 1-\widehat{Y_i} ))$$ Le problème d'optimisation devient : $$ \min_W \dfrac{1}{M}\sum_{i=1}^M L_i(X,Y;W)$$
On veut trouver W qui minimise la fonction L alors on dérive et l'on trouve où la dérivée s'annule. $$\dfrac{\partial L}{\partial W} = 0 $$
Résoudre l'équation ci-dessus de manière analytique est difficile, vous pouvez essayer pour vous en convaincre. Un résolution approchée par descente de gradient reste néanmoins possible. Il suffit pour cela de calculer : $$\dfrac{\partial L}{\partial W}$$
Calcul de la dérivée partielle de L¶
On cherche la dérivée suivante : $\dfrac{\partial L}{\partial W_0} $ L est une composition de fonctions alors sa dérivée s'appuie sur la chaine de dérivation suivante : Soit $q(p(W_0))$ alors $$\dfrac{\partial q}{\partial W_0} = \dfrac{\partial q}{\partial p} \dfrac{\partial p}{\partial W_0}$$ La dérivée de la fonction $log(x)$ est égale à $\dfrac{\partial log(x)}{\partial x} =\dfrac{1}{x}$.
La dérivée de la fonction $sigmoid(x)$ est égale à $\dfrac{\partial sigmoid(x)}{\partial x} =sigmoid(x) . (1-sigmoid(x))$.
Calcul de la dérivée partielle
$q_1=L_i=-(Y_i \log (\widehat{Y_i}) + (1-Y_i) \log( 1-\widehat{Y_i} ))$ et $p_1=\widehat{Y_i}$ donc $q_1=-(Y_i \log (p_1) + (1-Y_i) \log( 1-p_1) )$
$\dfrac{\partial q_1}{\partial W_0} = \dfrac{\partial q_1}{\partial p_1} \dfrac{\partial p_1}{\partial W_0}=(-\dfrac{Y_i}{\widehat{Y_i}}+\dfrac{1-Y_i}{1-\widehat{Y_i}})\dfrac{\partial p_1}{\partial W_0}$
$q_2=\widehat{Y_i}=sigmoid(z_i)$ et $p_2=z_i$ donc $q_2=sigmoid(z_i)$
$\dfrac{\partial q_2}{\partial W_0} = \dfrac{\partial q_2}{\partial p_2} \dfrac{\partial p_2}{\partial W_0}=sigmoid(z_i)*(1-sigmoid(z_i)) \dfrac{\partial p_2}{\partial W_0}$
$q_3=z_i$ et $p_3=z_i=X_{i,0}*W_0+X_{i,1}*W_1$ donc $q_3=p3$
- $\dfrac{\partial q_3}{\partial W_0} = \dfrac{\partial p_3}{\partial W_0}$=$X_{i,0}$
Résultat Final : $$\dfrac{\partial L_i}{\partial W_0}= (-\dfrac{Y_i}{\widehat{Y_i}}+\dfrac{1-Y_i}{1-\widehat{Y_i}}) (sigmoid(z_i)*(1-sigmoid(z_i)))X_{i,0}$$ $$\dfrac{\partial L_i}{\partial W_0}= (-\dfrac{Y_i}{\widehat{Y_i}}+\dfrac{1-Y_i}{1-\widehat{Y_i}}) (\widehat{Y_i}*(1-\widehat{Y_i}))X_{i,0}$$
$$\dfrac{\partial L_i}{\partial W_0}= (\widehat{Y_i} -Y_i) X_{i,0}$$
La version matricielle :
$$\dfrac{\partial L}{\partial W}= X^T(\widehat{Y} -Y) $$
Régression Logistique :Descente de Gradient Matricielle¶
def gradient (X,Y,W,pas,nbiter,M,maxy) :
for t in range (0,nbiter):
Z=X.dot(W)
Ypred=sigmoid(Z)
ecart=Ypred-Y
XT=X.transpose()
grad=XT.dot(ecart)
W = W -pas*grad
print('Itération numéro ',t)
print('Erreur : ',err)
return W, err
A vous de jouer¶
Classifier les images de piétons avec la nouvelle fonction à minimiser (la cross entropy)
Faire un programme dans Spyder qui classifie les images de piétons. Vous apprendrez sur les données suivantes : X=trainfeatures Y=trainlabels Afficher l'erreur (attention la cross entropy) et le taux de bonnes classifications par itération.
Tester votre prédicteur sur : X=trainfeatures Y=trainlabels Afficher l'erreurr et le taux de bonnes classifications
Puis sur Tester votre prédicteur sur : X=testfeatures Y=testlabels Afficher l'erreurr et le taux de bonnes classifications par itération.
Le but est d'évaluer la capacité du prédicteur à prédire sur de nouvelles données (jamais vue)